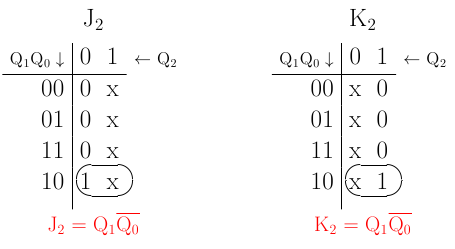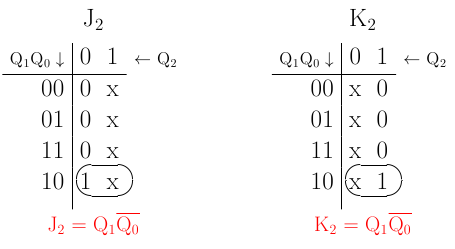ENUNCIADO
En el año 2718, la humanidad ha sido capaz de explorar numerosos
sistemas planetarios lejanos sin haber encontrado vida
inteligente1.
Los científicos deciden dejar dispositivos en los planetas visitados
que den pistas de la localización de la Tierra a otros viajeros
interestelares. Para que el visitante tenga constancia de que el objeto
que ve es producto de vida inteligente y no del azar, se decide que debe
llevar un contador que cuente según el inicio de la sucesión
de Fibonacci, en la que cada término resulta ser la suma de los
dos anteriores:
0, 1, 1, 2, 3, 5, 8, 13, y vuelta a empezar.
Nuestro cometido es diseñar tal contador. Después de mucho
recapacitar, se decide que se va a realizar el dispositivo como un
contador de cuatro bits de cuenta arbitraria. Sin embargo, nos encontramos con
el problema de que hay un número que se repite (el 1). Se decide
solucionarlo usando para el primer 1 otro número no usado (el 9)
e intentar corregir esa salida con lógica combinacional añadida
al final. De este modo, la cuenta que se debe generar es:
0, 9, 1, 2, 3, 5, 8, 13, y vuelta a empezar.
Veamos los pasos que hay que dar, recordando el ejemplo visto en teoría:
- Debemos construir el diagrama de transición de estados,
haciendo que los estados no usados decaigan a cualquiera de los
otros. De una elección acertada de estos decaimientos puede
depender lo simple o complicado que resulte el circuito final y,
dada la gran cantidad de planetas con posibilidad de vida, unos
céntimos de ahorro puede suponer un gran pellizco al final.
Este es el diagrama del ejemplo que veíamos en teoría:
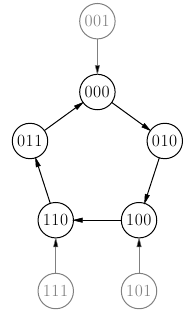
- Con ayuda de la tabla de transiciones del biestable JK,
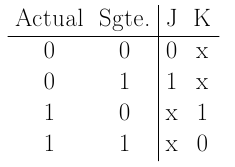 se debe escribir la tabla de transiciones. En el ejemplo de la
teoría, era:
se debe escribir la tabla de transiciones. En el ejemplo de la
teoría, era:

- Toca ahora escribir las jotas y las kas de los biestables en
función de las variables binarias que determinan el estado.
Estas variables son, en este ejercicio, las salidas de los
biestables: Q3Q2Q1Q0.
Nos podemos auxiliar de mapas de Karnaugh. Como muestra, parte del
ejemplo visto en teoría:
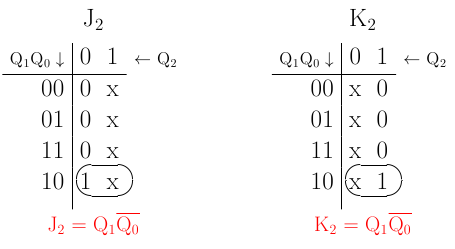
- Una vez deducidas las ecuaciones de excitación de las jotas y
las kas de cada biestable, se puede construir el circuito. En el ejemplo
de teoría, este es el circuito resultante:
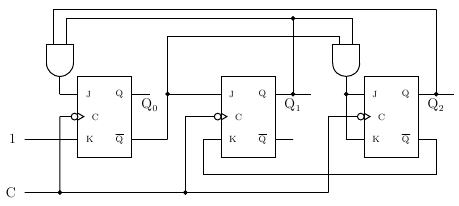
- Probad con Verilog el circuito que habéis obtenido. En caso
de que no realice la cuenta: 0, 9, 1, 2, 3, 5, 8, 13, 0, ...,
revisad los cálculos.
- Diseñad el circuito combinacional que cambie el 9 por un 1,
dejando el resto de valores que importan como está.
Si no sois capaces
de diseñarlo sobre la marcha, construid la tabla de verdad y
aplicad de nuevo los mapas de Karnaugh.
- Probad el diseño final y, de funcionar, disfrutad de vuestra
obra: un flamante señalador de vida inteligente para
extraterrestres2,
marca ACME®.
_____________________________
1 Esto supuso un duro revés para el
proyecto encargado
de la búsqueda de vida inteligente, al cual se dedicaron no pocos fondos.
Para evitar la tragedia política, se votó
y se aprobó, por ley, que se había demostrado que no había vida
inteligente en el Universo.
No se sabe bien si a propósito o no, no se hizo salvedad respecto al
planeta Tierra...
2 En el año 3141 parece que el dispositivo
tuvo éxito pues se recibió por radio cuántica un mensaje
de respuesta. La celebración fue grandiosa, aun sin haber sido capaz de
descifrar el mensaje. Por supuesto que se revocó la ley que afirmaba que no
había vida inteligente en el Universo y se levantaron múltiples
estatuas. El mensaje se vio que estaba compuesto por dos partes claramente diferenciadas.
Lo que parecía un saluda y una segunda parte algo más extensa que
podría ser un manual técnico avanzado con los descubrimientos
científicos de la civilización alienígena.
Al final, después de mucho esfuerzo, se logró
descifrar el mensaje corto. Venía a decir: "Vayan ya dejando de
abandonar chismes electrónicos. Nos estamos gastando un pastón
limpiando los planetas por donde van pasando". La traducción de la
segunda parte se abandonó al descubrir, justo al principio, las palabras:
"En la
oscuridad sonaba un teléfono, un sonido débil"...
COMENTARIOS
La primera solución y, de momento, la única, es la presentada
por Cunart (2010). Merece la pena que la echéis un vistazo por lo bien
documentada que está.
Presenta el autor, en realidad, dos soluciones, una primera, que usa:
- 4 biestables JK -> 24 puertas
- 5 puertas AND de 3 entradas -> 7.5 puertas
- 8 puertas AND de 2 entradas -> 8 puertas
- 1 puerta OR de 3 entradas -> 1.5 puertas
- 6 puertas OR de 2 entradas -> 6 puertas
En total, el equivalente a 47 puertas, según las condiciones del
ejercicio. Reproducimos el ejercicio, citando en cursiva, las palabras
de su autor.
Comenzamos dibujando el diagrama de transicción de estados
buscando que haya la mínima variación de bits entre los
estados que no pertenecen a la serie y los que sí. El diagrama
que he elegido en este caso es el siguiente:
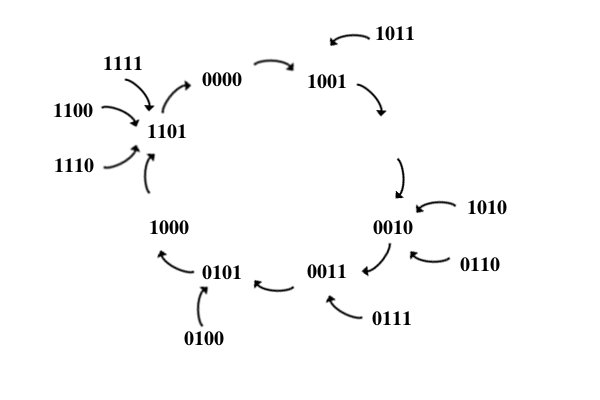 A partir del diagrama se hace la tabla de transiciones y se
escriben las J y K de los biestables en función de las
salidas de los mismos Q3, Q2, Q1, Q0:
A partir del diagrama se hace la tabla de transiciones y se
escriben las J y K de los biestables en función de las
salidas de los mismos Q3, Q2, Q1, Q0:
| J3 K3 | J2 K2 | J1 K1 | J0 K0 |
|---|
| 0000→1001 | 1 x |
0 x |
0 x |
1 x |
| 0001→0010 | 0 x |
0 x |
1 x |
x 1 |
| 0010→0011 | 0 x |
0 x |
x 0 |
1 x |
| 0011→0101 | 0 x |
1 x |
x 1 |
x 0 |
| 0100→0101 | 0 x |
x 0 |
0 x |
1 x |
| 0101→1000 | 1 x |
x 1 |
0 x |
x 1 |
| 0110→0011 | 0 x |
x 1 |
x 0 |
0 x |
| 0111→0011 | 0 x |
x 1 |
x 0 |
x 0 |
| 1000→1101 | x 0 |
1 x |
0 x |
1 x |
| 1001→0001 | x 1 |
0 x |
0 x |
x 0 |
| 1010→0010 | x 1 |
0 x |
x 0 |
0 x |
| 1011→1001 | x 0 |
0 x |
x 1 |
x 0 |
| 1100→1101 | x 0 |
x 0 |
0 x |
1 x |
| 1101→0000 | x 1 |
x 1 |
0 x |
x 1 |
| 1110→1101 | x 0 |
x 0 |
x 1 |
1 x |
| 1111→1101 | x 0 |
x 0 |
x 1 |
x 0 |
No dibujo los mapas de Karnaugh en este ejemplo, pongo tan solo
los resultados:
| J3= Q0Q1Q2+Q0Q1Q3 |
K3= Q0Q1+Q0Q2 |
| J2= Q0Q1Q3+Q0Q1Q3 |
K2= Q0Q1+Q1Q3 |
| J1= Q0Q2Q3 |
K1= Q0Q3+Q2Q3+Q0Q2 |
| J0= Q0+Q1 |
K0= Q1Q3+Q1Q2= Q1(Q2+Q3) |
Algunas se podrían reducir más, pero por estar repetidas
en más de una entrada es más rentable así. Una vez
que se tienen se puede dibujar el circuito resultante e implementarlo
en Verilog.
Para cambiar el 9 por el 1 he utilizado un circuicirto combinacional
sencillo consistente en dos puertas AND y una OR:
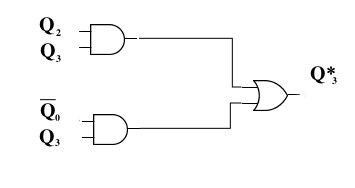
[[Como efecto colateral, el 11 también cambia al 3,
lo que no tiene importancia, pues el 11 no se usa en la cuenta]]
| Q | Q3Q2Q1Q0 |
Q3* |
Q3*Q2Q1Q0 |
Q* |
|---|
| 0 | 0000 | 0 | 0000 | 0 |
| 1 | 0001 | 0 | 0001 | 1 |
| 2 | 0010 | 0 | 0010 | 2 |
| 3 | 0011 | 0 | 0011 | 3 |
| 4 | 0100 | 0 | 0100 | 4 |
| 5 | 0101 | 0 | 0101 | 5 |
| 6 | 0110 | 0 | 0110 | 6 |
| 7 | 0111 | 0 | 0111 | 7 |
| 8 | 1000 | 1 | 1000 | 8 |
| 9 | 1001 | 0 | 0001 | 1 |
| 10 | 1010 | 1 | 1010 | 10 |
| 11 | 1011 | 0 | 0011 | 3 |
| 12 | 1100 | 1 | 1100 | 12 |
| 13 | 1101 | 1 | 1101 | 13 |
| 14 | 1110 | 1 | 1110 | 14 |
| 15 | 1111 | 1 | 1111 | 15 |
[[Nota del profesor]]
La imagen siguiente es cómo quedaría el diseño del circuito,
una maraña de cables:

Y este es el código presentado para esta primera solución:
/*
Computadores I - GII - USAL
Sesión 10 - Ejercicio 1.
Se nos pide diseñar un circuíto que siga la serie de Fibonacci
usando el menor número de puertas.
En esta solución se incluyen:
5 AND de tres entradas
8 AND de dos entradas
1 OR de tres entradas
7 OR de dos entradas
4 biestables JK
===========
48 puertas.
Por: cunart - Grupo A2
*/
//Modulo del biestable JK
module JKdown(output reg Q, output wire NQ, input wire J, input wire K, input wire C);
not(NQ,Q);
initial
begin
Q=0;
end
always @(posedge C)
case ({J,K})
2'b10: Q=1;
2'b01: Q=0;
2'b11: Q=~Q;
endcase
endmodule
//Módulo que contiene el contador y la circuitería auxiliar.
module contador (output wire[3:0] Q, input wire C);
//Cables correspondientes a las salidas negadas de los biestables.
wire [3:0] nQ;
//Cables que almacenan la salida temporal del biestable jk3.
wire Qt, nQt;
//Cables de entrada a los biestables.
wire wJ3, wK3, wJ2, wK2, wJ1, wK1, wJ0, wK0;
//Cables intermedios.
wire wq0n1q2, wn0n1n2, wq0n2, wq0n1, wn0n1q3, wq0q1n3, wq1n3, wq0q3;
wire wn2q3, wq2n3, wq2q3, wn0q3;
//Puertas correspondientes al contador.
and q0n1q2 (wq0n1q2, Q[0], nQ[1], Q[2]);
and n0n1n2 (wn0n1n2, nQ[0], nQ[1], nQ[2]);
or J3 (wJ3, wn0n1n2, wq0n1q2);
and q0n2 (wq0n2, Q[0], nQ[2]); //La salida va a K3 y K1.
and q0n1 (wq0n1, Q[0], nQ[1]); //La salida va a este y al K2.
or K3 (wK3, wq0n1, wq0n2);
and n0n1q3 (wn0n1q3, nQ[0], nQ[1], Qt);
and q0q1n3 (wq0q1n3, Q[0], Q[1], nQt);
or J2 (wJ2, wq0q1n3, wn0n1q3);
and q1n3 (wq1n3, Q[1], nQt);
or K2 (wK2, wq0n1, wq1n3);
and J1 (wJ1, Q[0], nQ[2], nQt);
and q0q3 (wq0q3, Q[0], Qt);
and n2q3 (wn2q3, nQ[2], Qt);
or K1 (wK1, wq0q3, wn2q3, wq0n2);
or J0 (wJ0, nQ[0], nQ[1]);
or q2n3 (wq2n3, Q[2], nQt);
and K0 (wK0, nQ[1], wq2n3);
JKdown jk0 (Q[0], nQ[0], wJ0, wK0, C);
JKdown jk1 (Q[1], nQ[1], wJ1, wK1, C);
JKdown jk2 (Q[2], nQ[2], wJ2, wK2, C);
JKdown jk3 (Qt, nQt, wJ3, wK3, C);
//Circuitería que cambia el nueve por el uno.
and q2q3 (wq2q3, Q[2], Qt);
and n0q3 (wn0q3, nQ[0], Qt);
or NQ3 (Q[3], wq2q3, wn0q3);
endmodule
//Módulo para probar el circuito.
module test;
reg I, C;
wire [3:0] Q;
contador counter (Q,C);
always
begin
#10 C=~C;
end
initial
begin
$dumpfile("ej1_48.dmp");
$dumpvars(2, counter, Q);
C=0;
#500 $finish;
end
endmodule
La segunda solución presentada no sigue estrictamente el camino
esbozado por el enunciado del ejercicio, sino que actúa de manera
más inteligente. Al fin y al cabo, si nos atamos desde
el principio a un diagrama de transición de estados, podemos
estar desaprovechando la oportunidad de elegir otro mejor. Así que,
el autor decide dejar flotanto los estados finales de aquellos que no
forman parte de la secuencia. Con lo único que hay que tener
precaución es con que los estados no usados decaigan siempre
a estados del contador, para evitar problemas en la indeterminación
en el encendido. ¿Habrá considerado esto el autor?
Sigamos, de nuevo, sus comentarios acerca de esta brillante solución:
Para obtener una solución con menor número de puertas,
en lugar de comenzar por el diagrama, lo hice por la tabla de
transiciones para los valores del ciclo y dejando como x el resto:
| J3 K3 | J2 K2 | J1 K1 | J0 K0 |
|---|
| 0000→1001 | 1 x |
0 x |
0 x |
1 x |
| 0001→0010 | 0 x |
0 x |
1 x |
x 1 |
| 0010→0011 | 0 x |
0 x |
x 0 |
1 x |
| 0011→0101 | 0 x |
1 x |
x 1 |
x 0 |
| 0100→xxxx | x x |
x x |
x x |
x x |
| 0101→1000 | 1 x |
x 1 |
0 x |
x 1 |
| 0110→xxxx | x x |
x x |
x x |
x x |
| 0111→xxxx | x x |
x x |
x x |
x x |
| 1000→1101 | x 0 |
1 x |
0 x |
1 x |
| 1001→0001 | x 1 |
0 x |
0 x |
x 0 |
| 1010→xxxx | x x |
x x |
x x |
x x |
| 1011→xxxx | x x |
x x |
x x |
x x |
| 1100→xxxx | x x |
x x |
x x |
x x |
| 1101→0000 | x 1 |
x 1 |
0 x |
x 1 |
| 1110→xxxx | x x |
x x |
x x |
x x |
| 1111→xxxx | x x |
x x |
x x |
x x |
Una vez tenemos esta tabla, escribimos los mapas de Karnaugh
para cada entrada de los biestables:
| J3 |
|---|
Q3Q2→
↓Q1Q0 |
00 | 01 | 11 | 10 |
|---|
| 00 | 1 |
x |
x |
x |
|---|
| 01 | 0 |
1 |
x |
x |
|---|
| 11 | 0 |
x |
x |
x |
|---|
| 10 | 0 |
x |
x |
x |
|---|
| J3= Q2 +
Q0
Q1
|
|
| J2 |
|---|
Q3Q2→
↓Q1Q0 |
00 | 01 | 11 | 10 |
|---|
| 00 | 0 | x |
x |
1 |
|---|
| 01 | 0 | x | x | 0 |
|---|
| 11 | 1 |
x |
x |
x |
|---|
| 10 | 0 | x |
x |
x |
|---|
| J2=
Q0
Q3
+
Q0 Q1
|
|
| J1 |
|---|
Q3Q2→
↓Q1Q0 |
00 | 01 | 11 | 10 |
|---|
| 00 | 0 | x | x | x |
|---|
| 01 | 1 |
0 | x | 0 |
|---|
| 11 | x |
x | x | x |
|---|
| 10 | x | x | x | x |
|---|
| J1=
Q0
Q2
Q3
|
|
| J0 |
|---|
Q3Q2→
↓Q1Q0 |
00 | 01 | 11 | 10 |
|---|
| 00 | 1 |
x |
x |
x |
|---|
| 01 | x |
x |
x |
x |
|---|
| 11 | x |
x |
x |
x |
|---|
| 10 | 1 |
x |
x |
x |
|---|
| J0=
1
|
|
| K3 |
|---|
Q3Q2→
↓Q1Q0 |
00 | 01 | 11 | 10 |
|---|
| 00 | x | x | x | 0 |
|---|
| 01 | x |
x |
1 |
1 |
|---|
| 11 | x |
x |
x |
x |
|---|
| 10 | x | x | x | x |
|---|
| K3=
Q0
|
|
| K2 |
|---|
Q3Q2→
↓Q1Q0 |
00 | 01 | 11 | 10 |
|---|
| 00 | x |
x |
x |
x |
|---|
| 01 | x |
1 |
1 |
x |
|---|
| 11 | x |
x |
x |
x |
|---|
| 10 | x |
x |
x |
x |
|---|
| K2=
1
|
|
| K1 |
|---|
Q3Q2→
↓Q1Q0 |
00 | 01 | 11 | 10 |
|---|
| 00 | x | x | x | x |
|---|
| 01 | x |
x |
x |
x |
|---|
| 11 | 1 |
x |
x |
x |
|---|
| 10 | 0 | x | x | x |
|---|
| K1=
Q0
|
|
| K0 |
|---|
Q3Q2→
↓Q1Q0 |
00 | 01 | 11 | 10 |
|---|
| 00 | x |
x |
x |
x |
|---|
| 01 | 1 |
1 |
1 |
0 |
|---|
| 11 | 0 |
x |
x |
x |
|---|
| 10 | x |
x |
x |
x |
|---|
| K0= Q2 +
Q1
Q3
|
|
Con esto podemos completar ahora la tabla de transiciones y el diagrama:
| J3 K3 | J2 K2 | J1 K1 | J0 K0 |
|---|
| 0000→1001 | 1 x |
0 x |
0 x |
1 x |
| 0001→0010 | 0 x |
0 x |
1 x |
x 1 |
| 0010→0011 | 0 x |
0 x |
x 0 |
1 x |
| 0011→0101 | 0 x |
1 x |
x 1 |
x 0 |
| 0100→1001 | 1 x |
x 1 |
0 x |
1 x |
| 0101→1000 | 1 x |
x 1 |
0 x |
x 1 |
| 0110→1011 | 1 x |
x 1 |
x 0 |
1 x |
| 0111→1000 | 1 x |
x 1 |
x 1 |
x 1 |
| 1000→1101 | x 0 |
1 x |
0 x |
1 x |
| 1001→0001 | x 1 |
0 x |
0 x |
x 0 |
| 1010→0011 | x 1 |
0 x |
x 0 |
1 x |
| 1011→0101 | x 1 |
1 x |
x 1 |
x 0 |
| 1100→0001 | x 1 |
x 1 |
0 x |
1 x |
| 1101→0000 | x 1 |
x 1 |
0 x |
x 1 |
| 1110→0001 | x 1 |
x 1 |
x 1 |
1 x |
| 1111→0000 | x 1 |
x 1 |
x 1 |
x 1 |
[[De hecho, podríamos completar mucho más la
tabla, pues como ya hemos realizado los mapas de Karnaugh, las x ya han
quedado completamente determinadas. Nota del profesor]]
[[Actualización 2018: una alumna desconocida descubrió un
error en la tabla anterior. Son las celdas en rojo. Muchas gracias por la aportación.
Aprovechemos para dar valores a
las x en función de lo obtenido en Karnaugh y, de paso, corregirlo:]]
| J3 K3 | J2 K2 | J1 K1 | J0 K0 | Final |
|---|
| 0000→???? | 1 0 |
0 1 |
0 0 |
1 1 | 1001 |
| 0001→???? | 0 1 |
0 1 |
1 1 |
1 1 | 0010 |
| 0010→???? | 0 0 |
0 1 |
0 0 |
1 0 | 0011 |
| 0011→???? | 0 1 |
1 1 |
1 1 |
1 0 | 0101 |
| 0100→???? | 1 0 |
0 1 |
0 0 |
1 1 | 1001 |
| 0101→???? | 1 1 |
0 1 |
0 1 |
1 1 | 1000 |
| 0110→???? | 1 0 |
0 1 |
0 0 |
1 1 | 1011 |
| 0111→???? | 1 1 |
1 1 |
0 1 |
1 1 | 1000 |
| 1000→???? | 1 0 |
1 1 |
0 0 |
1 0 | 1101 |
| 1001→???? | 0 1 |
0 1 |
0 1 |
1 0 | 0001 |
| 1010→???? | 0 0 |
1 1 |
0 0 |
1 0 | 1111 |
| 1011→???? | 0 1 |
1 1 |
0 1 |
1 0 | 0101 |
| 1100→???? | 1 0 |
1 1 |
0 0 |
1 1 | 1001 |
| 1101→???? | 1 1 |
0 1 |
0 1 |
1 1 | 0000 |
| 1110→???? | 1 0 |
1 1 |
0 0 |
1 1 | 1011 |
| 1111→???? | 1 1 |
1 1 |
0 1 |
1 1 | 0000 |
|
| J3= | Q2 +
Q0
Q1
|
| K3= | Q0 |
| J2= |
Q0 Q3 +
Q0 Q1
|
| K2= | 1 |
| J1= | Q0
Q2
Q3
|
| K1= | Q0 |
| J0= | 1 |
| K0= | Q2 +
Q1
Q3
|
|
El diagrama de estados resultante es el siguiente:
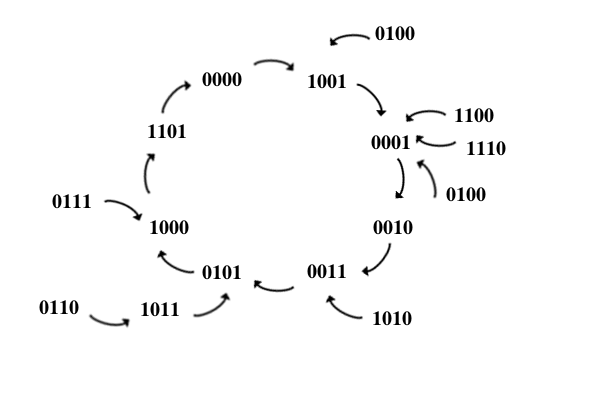 [[Afortunadamente, como se ve en el diagrama, no
se han producido ciclos entre los estados no usados, como explica el autor
dos párrafos más adelante. La solución
es, por tanto, válida. Nota del profesor.]]
[[Afortunadamente, como se ve en el diagrama, no
se han producido ciclos entre los estados no usados, como explica el autor
dos párrafos más adelante. La solución
es, por tanto, válida. Nota del profesor.]]
[[Actualización 2018: el diagrama de estados
estaba mal por dos motivos:
- Se basaba en los datos de una tabla que estaba mal
- Ni siquiera estaba correcto considerando los datos de esa tabla
(El 0100 estaba repetido. ¿Dónde estaba el 1111?...)
Esperemos que el siguiente sea correcto:
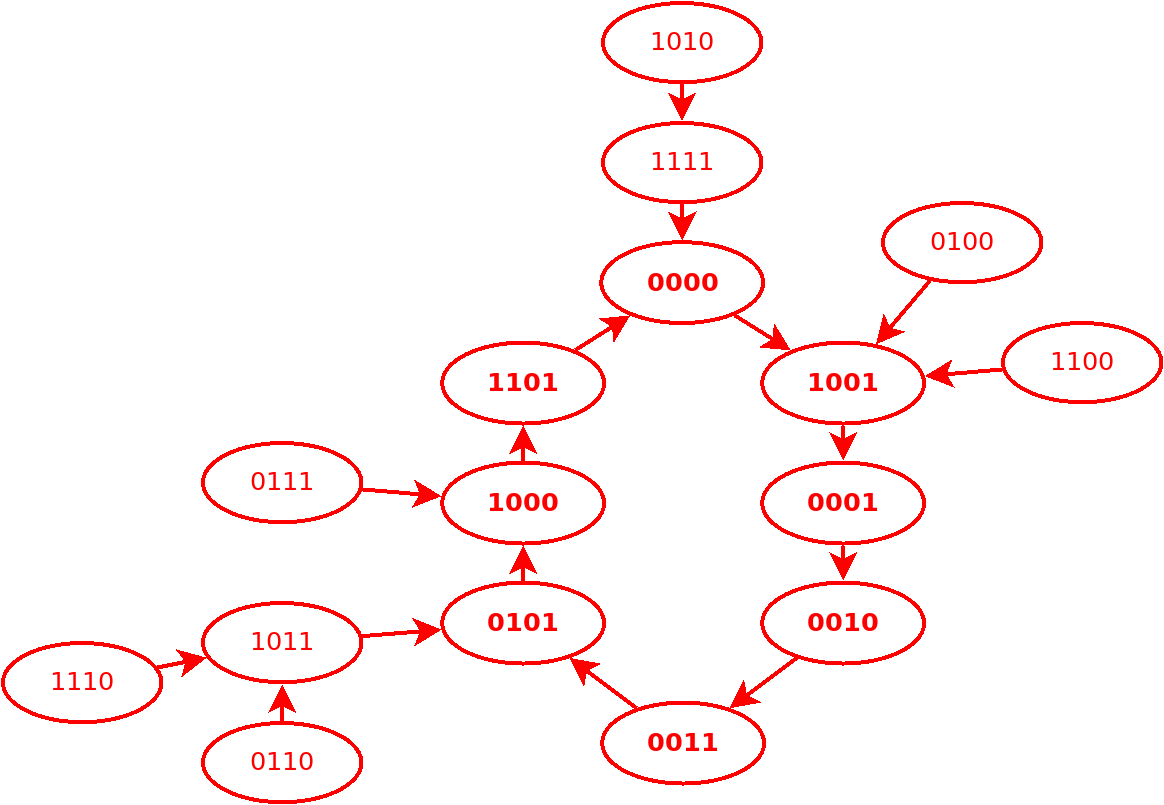 ]]
]]
Se podría hacer que del estado 0110 pasara directamente al ciclo,
pero esto supondría un aumento de puertas que se utilizarían
constantemente mientras que así, aunque se entre al ciclo en dos pasos,
es algo que ocurrirá solo puntualmente.
Es importante también fijarse en este punto en que podría haber
dos estados fuera del ciclo que formaran otro bucle externo (Ej.: 1011 →
0111 → 1010 → 0110) puesto que no se parte de un diagrama conocido.
Se debe por tanto comprobar que todos los estados externos acaben cayendo a
uno que pertenezca a la serie de Fibonacci. En ese caso habría que
retocar la tabla de forma que no ocurriera, pero en el diagrama de esta
solución se ve claro que esto no ocurre.
El circuito que se utiliza para pasar del 9 al 1 es el mismo que en el
apartado anterior, pero en este caso se podría ahorrar una puerta
AND, puesto que hemos usado la misma puerta (and n0q3) en
la parte anterior:

Y este es el código en Verilog:
/* Computadores I - GII - USAL
Sesión 10 - Ejercicio 1.
Se nos pide diseñar un circuíto que siga la serie de Fibonacci
usando el menor número de puertas.
En esta solución se incluyen:
1 AND de tres entradas
5 AND de dos entradas
4 OR de dos entradas
4 biestables JK
===========
34.5 puertas.
Por: cunart - Grupo A2
*/
//Modulo del biestable JK
module JKdown(output reg Q, output wire NQ, input wire J, input wire K, input wire C);
not(NQ,Q);
initial
begin
Q=0;
end
always @(posedge C)
case ({J,K})
2'b10: Q=1;
2'b01: Q=0;
2'b11: Q=~Q;
endcase
endmodule
//Módulo que contiene el contador y la circuitería auxiliar.
module contador (output wire [3:0] Q, input wire C);
//Cables correspondientes a las salidas negadas de los biestables.
wire [3:0] nQ;
//Cables que almacenan la salida temporal del biestable jk3.
wire Qt, nQt;
//Cables de entrada a los biestables.
wire wJ3, wJ2, wJ1, wK0;
//Cables intermedios.
wire wn0n1, wq0q1, wn0q3, wn3n1, wq2q3;
//Puertas correspondientes al contador.
and n0n1 (wn0n1, nQ[0], nQ[1]);
or J3 (wJ3, wn0n1, Q[2]);
and q0q1 ( wq0q1, Q[0], Q[1]);
and n0q3 ( wn0q3, nQ[0], Qt);
or J2 (wJ2, wq0q1, wn0q3);
and J1 (wJ1, nQ[2], nQt, Q[0]);
and n3n1 (wn3n1, nQt, nQ[1]);
or K0 (wK0, wn3n1, Q[2]);
JKdown jk1 (Q[0], nQ[0], 1'b1, wK0, C);
JKdown jk2 (Q[1], nQ[1], wJ1, Q[0], C);
JKdown jk3 (Q[2], nQ[2], wJ2, 1'b1, C);
JKdown jk4 (Qt, nQt, wJ3, Q[0], C);
//Circuitería adicional que cambia el nueve por el uno.
and q2q3 (wq2q3, Q[2], Qt);
or NQ3 (Q[3], wq2q3, wn0q3);
endmodule
//Módulo para probar el circuíto.
module test;
reg I, C;
wire [3:0] Q;
contador counter (Q,C);
always
begin
#10 C=~C;
end
initial
begin
$dumpfile("ej1_34-5.dmp");
$dumpvars(2, counter, Q);
C=0;
#500 $finish;
end
endmodule
La salida vista en el GTKWave es la siguiente:
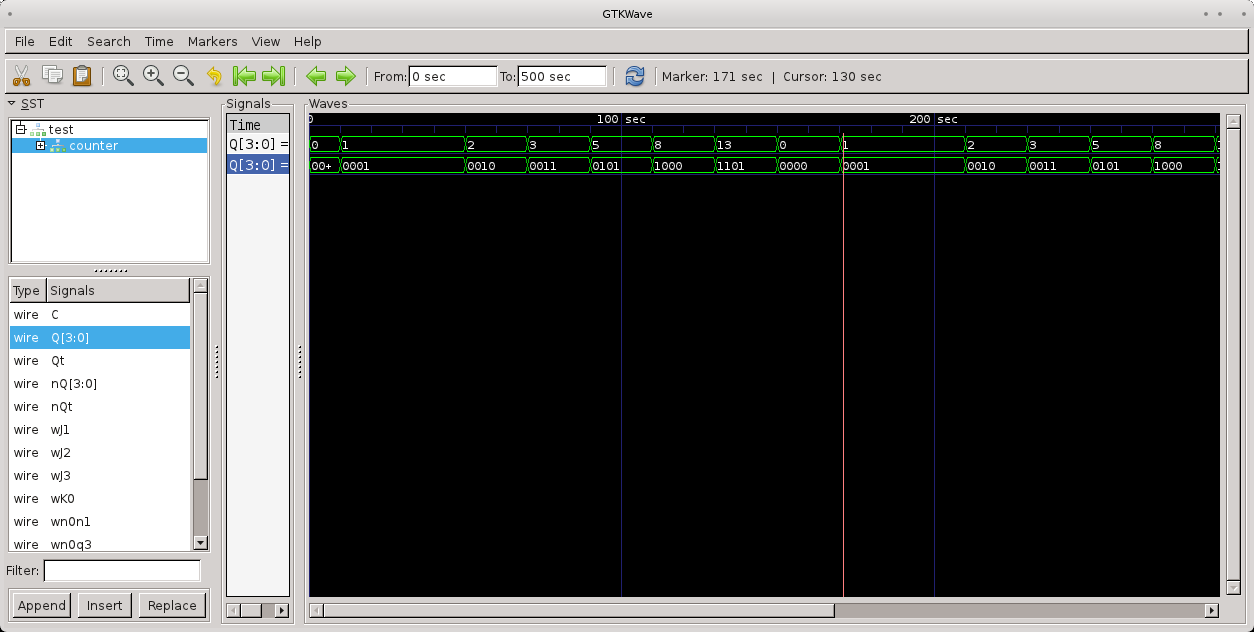
El circuito, realizado con el programa KTechLab, donde también se
comprueba su funcionamiento, es el siguiente:
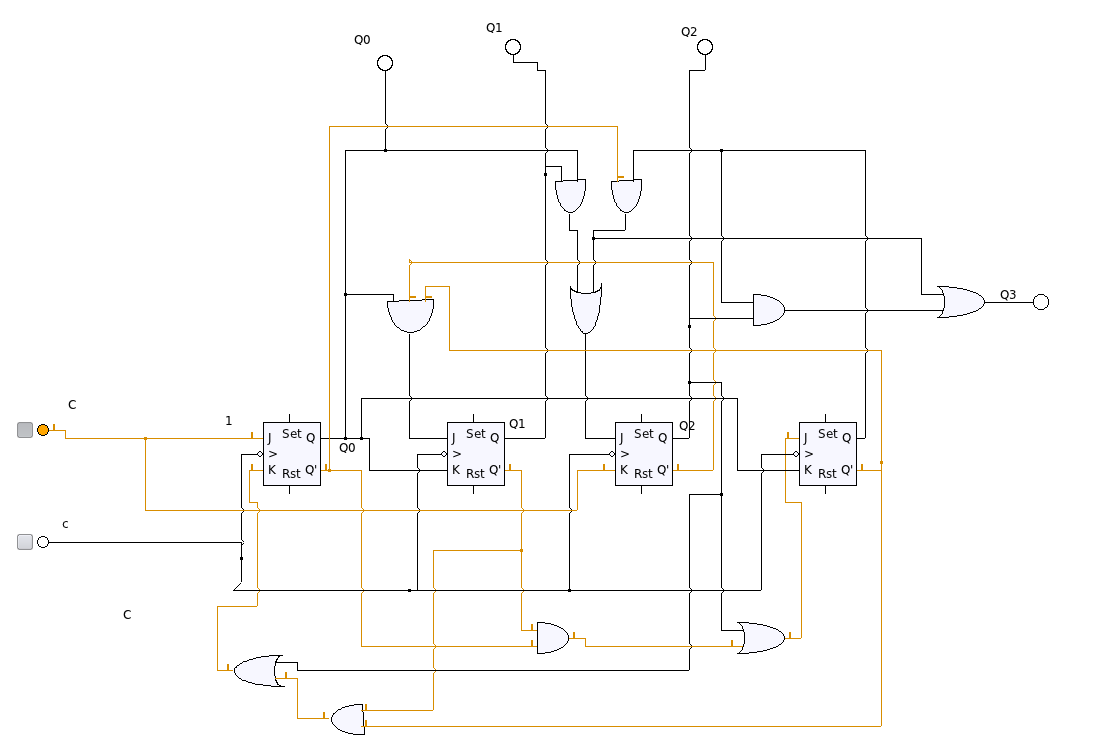
A la pregunta que se hace al final, sería un código como
el siguiente, útil en caso de que vayamos a útilizar este circuito
formando parte de otro mayor y ya tengamos el diseño listo:
module contador (output reg [3:0] Q, input wire C);
reg [3:0] Qt1; reg [3:0] Qt2;
initial
begin
Q = 13;
end
always @(posedge C)
begin
if (Q == 13)
begin
Q = 0; // En estos dos casos, se ignora el reloj.
#20 // Mejor sería hacer una tabla directa
Q = 1; // basándonos solo en el estado anterior:
#40 // 0 -> 1 -> 1 -> 2 -> 3 -> ...
Qt2 = 0; // y apañando algo para el 1 repetido
Qt1 = 1; // [[Nota del profesor]]
end
Q = Qt1 + Qt2;
Qt2 = Qt1;
Qt1 = Q;
end
endmodule
© 2011 Guillermo González Talaván, a excepción de
las prácticas presentadas por los alumnos