Mapas Autoorganizados

 

Los Mapas Autoorganizados son el segundo gran grupo de redes neuronales que trataremos. Probablemente sean, junto con el Perceptrón Multicapa, las redes más usadas.

 

MAPAS AUTOORGANIZADOS

En las redes autoorganizadas, el entrenamiento se realiza presentando sólo entradas. Como resultado de este aprendizaje no supervisado (también a veces se les llama redes no supervisadas), la red debe descubrir patrones o características significativas en los datos de entrada, e incorporarlas a sus pesos (autoorganización).

Este tipo de procesamiento es muy útil para distintos tipos de aplicaciones: análisis de similitud de patrones de entrada (reconocimiento de imagen, sonido, etc.); análisis de componentes principales, agrupamiento y clasificación, memoria asociativo, codificación, etc.

La regla de aprendizaje más utilizada por las redes autoorganizadas es el aprendizaje competitivo. Es la base de las redes de este tipo más utilizadas: ART (Grossberg 88), Neo-cognitrón (Fukushima 80) y los mapas autoorganizados (Kohonen 82,89). De estas redes, veremos los Mapas Autoorganizados, por ser las más usadas y porque el ART apenas se utiliza y el Neo-cognitrón es demasiado complicado para un primer acercamiento al tema.

La idea básica del aprendizaje competitivo es que una capa de elementos de proceso modifique sus pesos en Rⁿ de forma que su distribución de frecuencias sea proporcional a la densidad de probabilidad de los vectores de entrada.

La arquitectura es la siguiente:

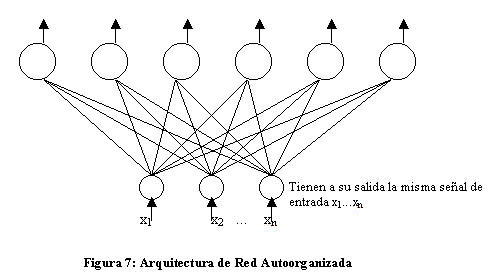
Tal y como se plantea la arquitectura, todas las neuronas de la capa de salida reciben las mismas entradas, que son el vector de entrada modificado por los pesos. Las neuronas de la capa de entrada son una mera excusa para crear el entramado de pesos.

La capa de salida tendrá m elementos de proceso, cada uno de los cuales recibe las mismas n señales x_i.

Cada EP calcula su intensidad de entrada I_i=D(w_i,x); donde D es una función de la medida de distancia entre los vectores de entrada x y de pesos w_i (suele usarse la distancia euclídea en el espacio Rⁿ, aunque existen otras como la distancia de Manhattan, el producto escalar normalizado, la distancia de Minkowsky, etc.).

Una vez se han calculado las intensidades, arranca una competición para ver qué neurona tiene la mínima intensidad, es decir, su vector de pesos está más próximo a la entrada; bien mediante inhibición lateral (cada neurona compara con sus neuronas vecinas) o de forma centralizada (una neurona o elemento externo mide todas las distancias).

La salida de la neurona ganadora se hace 1, mientras el resto se iguala a 0.

A continuación se aplica la ley de Kohonen:

            w_i(k+1) = w_i(k) + a (x-w_i(k))z_i         

, con a constante en [0,1], llamada factor de aprendizaje

 Debido a z_i, está claro que sólo el vector de pesos de la neurona ganadora se modificará, “moviéndose” hacia el vector de entrada. A medida que se introducen entradas, los vectores de pesos van formando nubes que siguen la distribución de las entradas.

 Existe el problema de que la ley de Kohonen no produce, en general, un conjunto de vectores de peso equiprobables (es decir, ante un vector de entrada x, no todas las neuronas tienen la misma posibilidad de ganar).

 El mapa autoorganizado usa una variante del aprendizaje competitivo en el que, además de actualizar los pesos de la neurona ganadora, se actualizan también los de las neuronas vecinas, de forma proporcional a la cercanía a la que se encuentren, según una cierta función de vecindad h.

 h(i,g) -siendo g la neurona ganadora y sus vecinas i- decrece con la distancia (i-g) y depende de una parámetro llamado radio de vecindad R(t), un número entero a partir del cual las neuronas situadas a una distancia mayor no modifican sus pesos.

 Tanto el factor de aprendizaje a como R(t) van decreciendo a medida que progresa el entrenamiento.

 Para determinar el grado de vecindad, aunque todas las neuronas de salida se dispongan en una sola capa, se distribuyen con una estructura de una dimensión (lineal), dos (planar) o tres (espacial).

 Como resultado del proceso de entrenamiento, las neuronas se van sintonizando de forma selectiva a los patrones de entrada, Un SOM forma un mapa topográfico de los patrones de entrada, en el que las coordenadas de las neuronas corresponden a características intrínsecas en dichos patrones.